■ Neural Networks: Data normalization
http://www.cs.sunysb.edu/~cse634/ch6NN.pdf
뉴럴 네트워크에서는 입력과 출력 데이터의 정규화가 필요하다. 위 사이트에 보면 데이터 정규화 방법으로 두개가 나와 있다.
All values of attributes in the dataset has to be changed to contain values in the interval [0,1], or [-1,1].
모든 데이터는 0~1, -1~1 사이 값에 포함되도록 바꿔야 한다.
Two basic normalization techniques:
- Max-Min normalization
- Decimal Scaling normalization
Max-Min normalization formula
Example: We want to normalize data to range of the interval [0,1].
We put: new_max A=1, new_min A = 0
Say, max A was 100 and min A was 20(That means maximum and minimum values for the attribute A).
Now, if v=40(if for this particular pattern, attribute value is 40), v' will be calculated as,
v'=(40-20)*(1-0)/(100-20)+0
= (20 * 1)/80
= 0.4(?) 아닌거 같은데... 0.25 아닌가?!!
Decimal Scaling Normalization formula
where j is the smallest integer such that max|v’|<1.
Example :
A–values range from -986 to 917. Max |v| = 986.
v = -986 normalize to v’= -986/1000 = -0.986
'PatternRecognition' 카테고리의 다른 글
| Linear Discriminant Analysis(LDA) - C-Classes (0) | 2014.06.02 |
|---|---|
| Linear Discriminant Analysis(LDA) - 2 classes (0) | 2014.05.30 |
| The Basic Artificial Neuron: Bias neuron(Backpropagation) (3) | 2014.04.23 |
| 기초 통계(Statistic) (0) | 2014.04.14 |
| Principal Component Analysis(주성분 분석) (0) | 2014.04.12 |
■ The Basic Artificial Neuron: Bias neuron(Backpropagation)
역전파 알고리즘 - 바이어스 노드
역전파 알고리즘은 각 뉴런의 출력 신호를 결정하기 위해서 입력(입력 신호와 연결 무게를 곱하고 나서 모두 합한값)에 활성화 함수(Activation Function)를 적용한다.
- 활성화 함수의 임계값 변동을 흡수하기 위한 가중치를 바이어스(편견)이라고 하며, 항상 1의 값을 가진다.
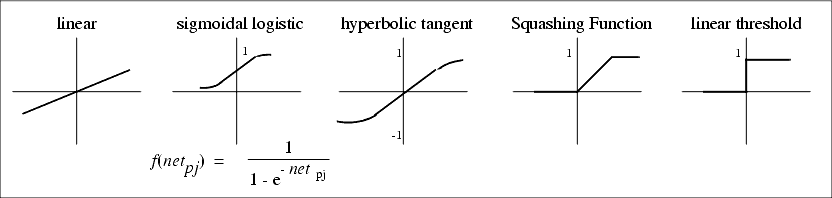
여러 활성화 함수 그림이다.
여기서 질문이 생긴다. 활성화 함수의 임계값 변동을 흡수(?-책에서 이렇게 씀)하기 위한 가중치 바이어스 노드를 항상 1로 설정한다라고 되어 있는데 왜 1인가 그리고 구체적인 이유가 무엇인가?
우선 구글링 한 정보를 정리하면 다음과 같다.
http://stackoverflow.com/questions/2480650/role-of-bias-in-neural-networks
http://stackoverflow.com/questions/8039313/why-is-a-bias-neuron-necessary-for-a-backpropagating-neural-network-that-recogni
답변에 보면 바이어스 값(bias value)는 성공적인 학습을 위해 활성화 함수를 좌우로 움직일 수 있게 해준다라고 한다. 단순한 예제를 보면 다음과 같다.
Case 1 : 바이어스 없이 하나의 입력과 출력의 구성

출력은 입력 x와 가중치 w0의 곱을 활성화 함수에 넣어 계산할 수 있다.

위 그림은 활성화 함수를 sigmoid로 하고 가중치 w0의 값이 0.5, 1.0, 2.0으로 변화 할때 입력과 출력에 관한 결과 그래프 이다. 위 그래프에서 보면 가중치 값이 변화함에 따라 sigmoid 의 가파름(steepness) 정도가 변화는 것을 확인할 수 있다. 이 결과는 유용하지만 만약 입력이 2개이고 출력이 하나인 네트워크를 구성할때 변화하는 시그모이드 함수의 steepness는 동작하지 않는다고 한다. (먼 예기야?)
위 커브들을 오른쪽으로 모두 옴기길 원하면 바이어스를 사용해야 한다.
다음 case를 보고 차이점을 보자
Case2: Case1 + Bias Neuron

그림에 보면 입력층에 Bias Neuron을 추가된 것을 확인할 수 있다. 그럼 출력은 sig(w0*x+w1*1.0)으로 계산될 수 있다. 아래 그림은 w1의 변화에 따른 네트워크 출력에 대한 그래프이다. (w0 = 1.0)

그림에 보면 바이어스 뉴런을 하나 추가하여 가중치 w1의 변화에 따라 출력이 좌우로 움직이(shift)되는 것을 확인할 수 있다. 아하!!!(센스 있는 사람은 눈치 챘을 것이다.)
@user1621769: The main function of a bias is to provide every node with a trainable constant value (in addition to the normal inputs that the node recieves). You can achieve that with a single bias node with connections to N nodes, or with N bias nodes each with a single connection; the result should be the same. – Nate Kohl Mar 24 '13 at 13:24
위 빨간색을 보면 중요한 얘기를 하고 있다.
바이어스의 중요한 기능은 훈련 가능한 상수 값을 가지는 모든 노드를 제공하는 것이다.
즉 바이어스 노드 없이 훈련 가능한 것들도 있지만 아마 다른 경우에 sigmoid 임계 범위에 있지 않은 값들의 출력은 의미가 없어져 훈련이 되지 않을 수도 있다.
http://www.nnwj.de/backpropagation.html
위 사이트에서 보면 보다 이해하기 쉬울 것이다.
http://www.mathworks.co.kr/kr/help/nnet/ug/perceptron-neural-networks.html
여기 사이트에서도 bias 의 역할을 설명하고 있다. 바이어스의 또 다른 역할은 기본 영역에서 항상 시프트하여 경계를 결정하게 해 줌 아래와 같이 점선에서 실선으로 바이어스를 적용하여 경계를 옴김

그럼 실제 뉴럴 계층에 bias neuron을 어떻게 적용시켜야 하나 문제다. 다음 그림을 보자.
http://ufldl.stanford.edu/wiki/index.php/Neural_Networks
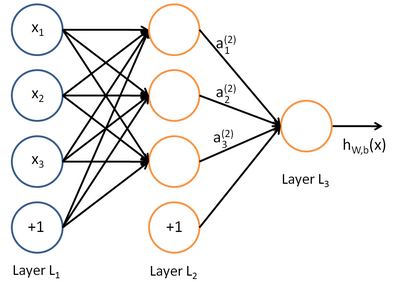
왼쪽 부터 입력 레이어(L1), 히든 레이어(L2), 출력 레이어(L3)로 나타난다. 보면 bias neuron이 입력과 히든레이어에 존재한다.
바이어스 뉴런은 다음 계층에 연결되지만 이전 계층에는 연결되지 않는 특징을 가진다.
입력층: 입력 노드(d) + 바이어스 노드(1)
은닉층: 은닉 노드(p) + 바이어스 노드(1)
은닉층의 노드 개수를 p라고 할때 하나의 바이어스 노드를 더해 은닉층의 총 노드 개수는 p+1개가 된다.
출력층: 원하는 출력 노드 수(m)
그럼 입력층과 은닉층 사이 가중치는 몇개?
입력층: d+1
은닉층: p
입력층과 은닉층의 가중치: (d+1)*p 개
그럼 은닉층과 출력층의 가중치는 몇개?
은닉층: p+1
출력층: m
은닉층과 출력층의 가중치: (p+1)*m 개
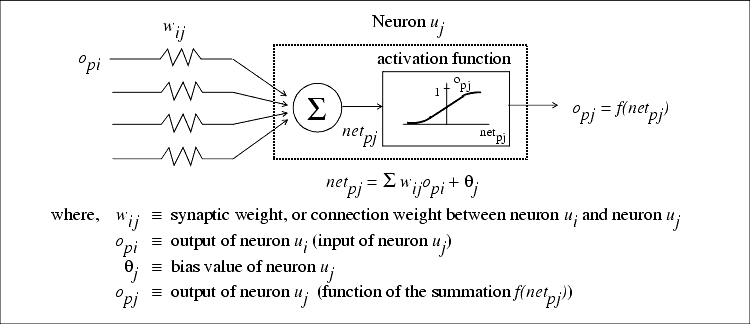
위 그림은 Basic Structure of an artificial neuron 그림이다. 맘에 들어서 가져 왔다. 자세한 설명은
http://engineeronadisk.com/book_modeling/neural.html
에 있다.
'PatternRecognition' 카테고리의 다른 글
| Linear Discriminant Analysis(LDA) - C-Classes (0) | 2014.06.02 |
|---|---|
| Linear Discriminant Analysis(LDA) - 2 classes (0) | 2014.05.30 |
| Neural Networks: Data normalization (0) | 2014.04.25 |
| 기초 통계(Statistic) (0) | 2014.04.14 |
| Principal Component Analysis(주성분 분석) (0) | 2014.04.12 |
◆ OpenGL: gluPerspective
원근 투영 방법
gluPerspective(GLdouble fovy, GLdouble aspect, GLdouble zNear, GLdouble zFar)
- 멀고 가까움을 표현함
- gluPerspective(시야각, 종횡비, 전방전달면, 후방절단면)
ex) gluPerspective(45.0, width/height, 1.0, 400.0);


http://warmz.tistory.com/440
시야(FOV: Field of View):상하 y축 방향의 시야각(0 -180도)
X축 방향의 시야는 종횡비(Aspect Ratio)에 의해 결정됨(폭 / 높이)
'OpenGL' 카테고리의 다른 글
| OpenGL: Index of Vertex Array (0) | 2014.05.04 |
|---|---|
| OpenGL: Geometric and Vertex (0) | 2014.05.04 |
| OpenGL: Setting Viewport (0) | 2014.04.19 |
| OpenGL: Setting Clipping region (0) | 2014.04.19 |
| OpenGL: Basic knowledge for 3D programing (0) | 2014.04.19 |






